A Contextual Hierarchical Attention Network with Adaptive Objective for Dialogue State Tracking

CHAN-DST

• slot imbalance 문제를 해결하고자 adaptive objective를 도입
• a contextual hierarchical attention network (CHAN)를 사용: dislogue history에서 relevant context를 찾기 위함
  → 각 턴의 발화로부터 word-level 관련 정보 검색
  → contextual representation으로 encode
  → 모든 context표현을 turn-level관련 정보로 집계한 후 word-level 정보와 합친 output 생성
• state transition prediction task

Definition

• $T$: turn
• $U_t$: user utterance of turn t
• $R_t$: system response of turn t
• $X$: $\left\{(U_1, R_1), ... , (U_T, R_T)\right\}$
• $B_t$: $\left\{(s, v_t), s \in S\right\}$
• $S$: set of slots
• $v_t$: corresponding value of the slot $s$
• slot: concatenation of a domain name and a slot name

Contextual Hierarchical Attention Network

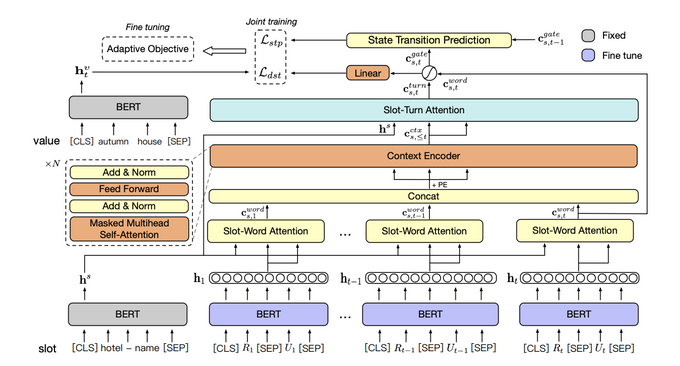
1. Sentence Encoder

utterance encoder

• BERT special token 사용
  → [CLS] : 문장의 representation들을 합치기위해 사용 (to aggregate the whole representation of a sentence)
  → [SEP] : 문장의 끝을 나타내기위해 사용.
• $U_t = \left\{w_1^u, ..., w_l^u\right\}$ (user utterance)
  $R_t = \left\{w_1^r, ..., w_{l'}^r\right\}$ (system response)
  $t$: dialogue turn
• $h_t = BERT_{finetune}([R_t;U_t])$
  ($h_t$: contextual word representations)
• 여기서 BERT finetune은 training도중 finetuning이 될것을 의미.

slot-value encoder

• $BERT_{fixed}$는 contextual semantics vectors로 encode해준다.
• utterance encode할때와 다른 점은 [CLS] 토큰의 output vector를 전체 문장 representation할때 사용한다. (to obtain the whole sentence representation)
• $h_s = BERT_{fixed}(s)$
  $h_t^v = BERT_{fixed}(v_t)$
• $BERT_{fixed}$는 training 도중 고정되어있다. 그래서 우리 모델은 unseen slots and values에 대해서 original BERT representation로 확장해서 보는게 가능하다.

2. Slot-Word Attention

• slot-word attention은 multi-head attention을 사용한다.
• $c_{s,t}^{word} = MultiHead(h^s, h_t, h_t)$

3. Context Encoder

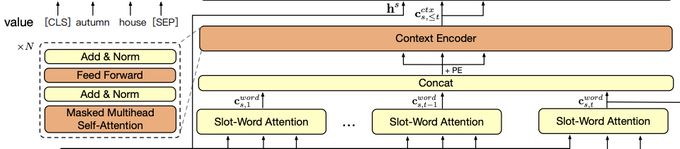
• context encoder : unidirectional transformer encoder
• {1, ..., t} 턴에서 추출 된 word-level slot-related 정보의 contextual relevance를 모델링하기 위한 것.

• $N$개의 idenctical한 layer가 있다.

  • 각 layer는 2개의 sub-layer를 가지고 있다.
  • 첫번째 sub-layer: masked multi-head self-attention(Q = K = V)
  • 두번째 sub-layer: position-wise fully connected feed-forward network(FFN) (two linear transformations, RELU activation으로 구성)
  • $FFN(x) = max(0, xW_1 + b_1)W_2 + b_2$
• $m^n = FFN(MultiHead(m^{n-1}, m^{n-1}, m^{n-1}))$
  $m^0 = [c_{s,1}^{word} + PE(1), ..., c_{s,t}^{word} + PE(t)]$
  $c_{s,\leq t}^{ctx} = m^N$
• $m^n$: n번째 context encoder레이어의 아웃풋 $PE(.)$: positional encoding function

4. Slot-Turn Attention

• turn-level relevant information을 contextual representation에서 검출해내기 위해 사용
• $c_{s,t}^{turn} = MultiHead(h^s, c_{s,\leq t}^{ctx},c_{s,\leq t}^{ctx})$
• 이로인해 word-level and turn-level 의 relevant information을 historical dialogues에서 얻어낼 수 있다.

5. Global-Local Fusion Gate

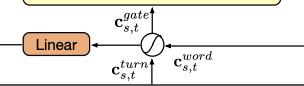
• global context와 local utterance의 균형을 맞추기 위해, contextual information과 current turn information의 비율을 조절함.
• $c_{s,t}^{word},~~ c_{s,t}^{turn}$에 따라 global과 local정보가 어떻게 결합되어야할지 알려주는 fusion gate mechanism을 사용
• $g_{s,t} = \sigma(W_g\bigodot[c_{s,t}^{word};c_{s,t}^{turn}])$

• $c_{s,t}^gate = g_{s,t}\bigotimes c_{s,t}^{word} + (1-g_{s,t}\bigotimes c_{s,t}^{turn})$

  • $W_g \in R^{2d\times d}$
  • $\sigma$: Sigmoid
  • $\bigodot$, $\bigotimes$
• $o_{s,t}$ = LayerNorm(Linear(Dropout($c_{s,t}^{gate}$)))

• value $v_t$에 대한 확률분포와 training objective
  $p(v_t|U_{\leq t},~R_{\leq t}, s) = exp(-||o_{s,t} - h_t^v||2)\over {\sum{v'\in V_s}exp(-||o_{s,t}-h_t^{v'}||2)}$
  $L{dst}$ $= \sum_{s\in S}\sum ^T_{t = 1}-log(p(\hat v_t|U_{\leq t},~R_{\leq t}, s))$

  • $V_s$: candidate value set of slot s
  • $\hat v_t \in V_s$: ground-truth value of slot s

State Transition Prediction

• relevant context를 더 잘 포착하기 위해, auxiliary binary classification task사용.
• $c_{s,t}^{stp} = tanh(W_c \odot c_{s,t}^{gate})$

• $p_{s,t}^{stp} = \sigma (W_p \odot [c_{s,t}^{stp};c_{s, t-1}^{stp}])$

  • $W_c \in \R^{d\times d}$
  • $W_c \in \R^{2d}$
  • $t = 1$일때는 $c_{s,t}^{stp}$와 zero vectors를 concat함.
• binary CE loss ($y_{s,t}^{stp}$: ground-truth transition labels // $p_{s,t}^{stp}$: transition probability)
• $L_{stp} = \sum_{s\in S}\sum_{t = 1}^T -y_{s,t}^{stp}~.~log(p_{s,t}^{stp})$

Adaptive Objective

• hard slots와 samples에 관한 optimization을 encourage한다.
• all slots의 learning을 balancing함.
• $acc_s^{val}$: accuracy of slot s on validation set

• slot-level difficulty if $acc_s^{val} \leq acc_{s'}^{val}$;
  → slot s 가 slot s'보다 더 어려운 것.
  → $\alpha$: slot-level difficulty

  • $\alpha_s = {1 - acc_s^{val} \over {\sum_{s'\in S} 1-acc_{s'}^{val}}} \cdot |S|$

• sample-level difficulty
  → Suppose there are two samples $\left\{(U_t, R_t),(s, v_t)\right\}$ and $\left\{(U_{t'}, R_{t'}),(s', v_{t'})\right\}$
  → 만약 former confidence 가 latter보다 더 낮다면, 첫번째 sample이 두번째보다 더 어려운 것.
  → $\beta$: sample level difficulty

  • $\beta(s, v_t) = (1 - p(s, v_t))^\gamma$
  • $p(s,v_t)$: confidence of sample $(U_t, R_t),(s, v_t)$
    $\gamma$: hyper-parameter
• $L_{adapt}(s,v_t) = -\alpha_s\beta(s, v_t)log(p(s, v_t))$
• slot s가 평균 slot의 difficulty보다 높다면, $\alpha_s$는 s에 대한 loss를 키울 것이다. 비슷하게, sample의 optimization이 low confidence를 갖고 있다면 loss는 커질것이다.

Optimization

• During joint training, we optimize the sum of these two loss functions as following
  $L_{joint} = L_{dst} + L_{stp}$
• At the fine-tuning phase, we adopt the adaptive objective to fine-tune DST task as following
  $L_{finetune} = \sum_{s\in S}\sum^T_{t=1}L_{adapt(s, \hat v_t)}$

참고 자료

• 논문: A Contextual Hierarchical Attention Network with Adaptive Objective for Dialogue State Tracking
• GitHub: CHAN-DST